Stack Overflow上最火的一段代码竟然有Bug

2010年的某一天,我忙中偷闲去Stack Overflow上赚声望值。
于是,我看到了下面这个问题:怎样将字节数输出成人类可读的格式?也就是说,怎样将123,456,789字节输出成123.5MB?
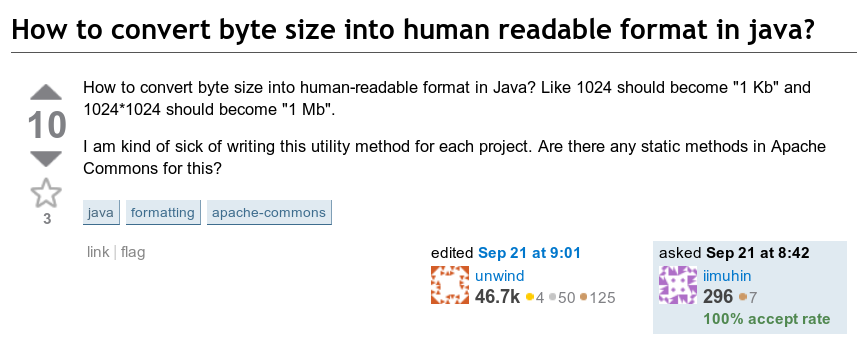
隐含的条件是,结果字符串应当在1~999.9的范围内,后面跟一个适当的表示单位的后缀。
这个问题已经有一个答案了,代码是用循环写的。基本思路很简单:尝试所有尺度,从最大的EB(10^18字节)开始直到最小的B(1字节),然后选择小于字节数的第一个尺度。用伪代码来表示的话大致如下:
suffixes = [ "EB", "PB", "TB", "GB", "MB", "kB", "B" ]magnitudes = [ 1018, 1015, 1012, 109, 106, 103, 100 ]i = 0while (i < magnitudes.length && magnitudes[i] > byteCount)i++printf("%.1f %s", byteCount / magnitudes[i], suffixes[i])
通常,如果一个问题已经有了正确答案,并且有人赞过,别的回答就很难赶超了。不过这个答案有一些问题,所以我依然有机会超过它。至少,循环还有很大的清理空间。

这只是一个代数问题!
然后我就想到,kB、MB、GB……等后缀只不过是1000的幂(或者在IEC标准下是1024的幂),也就是说不需要使用循环,完全可以使用对数来计算正确的后缀。
根据这个想法,我写出了下面的答案:
public static String humanReadableByteCount(long bytes, boolean si) {int unit = si ? 1000 : 1024;if (bytes < unit) return bytes + " B";int exp = (int) (Math.log(bytes) / Math.log(unit));String pre = (si ? "kMGTPE" : "KMGTPE").charAt(exp-1) + (si ? "" : "i");return String.format("%.1f %sB", bytes / Math.pow(unit, exp), pre);}
当然,这段代码并不是太好理解,而且log和pow的组合的效率也不高。但我没有使用循环,而且没有任何分支,看起来很干净。
这段代码的数学原理很简单。字节数表示为byteCount = 1000^s,其中s表示尺度。(对于二进制记法则使用1024为底。)求解s可得s = log_1000(byteCount)。
API并没有提供log_1000,但我们可以用自然对数表示为s = log(byteCount) / log(1000)。然后对s向下取整(强制转换为int),这样对于大于1MB但不足1GB的都可以用MB来表示。
此时如果s=1,尺度就是kB,如果s=2,尺度就是MB,以此类推。然后将byteCount除以1000^s,并找出正确的后缀。
接下来,我就等着社区的反馈了。我并不知道这段代码后来成了被复制粘贴最多的代码。

对于贡献的研究
到了2018年,一位名叫Sebastian Baltes的博士生在《Empirical Software Engineering》杂志上发表了一篇论文,题为《Usage and Attribution of Stack Overflow Code Snippets in GitHub Projects》。该论文的主旨可以概括成一点:人们是否在遵守Stack Overflow的CC BY-SA 3.0授权?也就是说,当人们从Stack Overflow上复制粘贴时,会怎么注明来源?
作为分析的一部分,他们从Stack Overflow的数据转出中提取了代码片段,并与公开的GitHub代码库中的代码进行匹配。论文摘要如是说:
We present results of a large-scale empirical study analyzing the usage and attribution of non-trivial Java code snippets from SO answers in public GitHub (GH) projects.
(本文对于在公开的GitHub项目中使用来自Stack Overflow上有价值的代码片段的情况以及来源注明情况进行了大规模的经验分析,并给出了结果。)
(剧透:绝大多数人并不会注明来源。)
论文中有这样一张表格:

id为3758880的答案正是我八年前贴出的答案。此时该答案已经被阅读了几十万次,拥有上千个赞。
在GitHub上随便搜索一下就能找到数千个humanReadableByteCount函数:
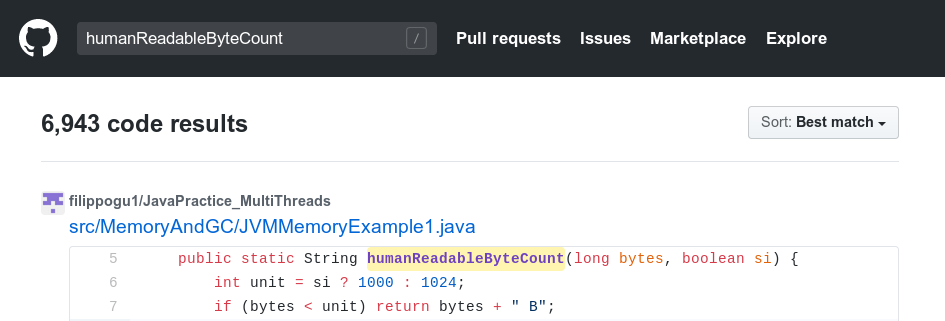
你可以用下面的命令看看自己有没有无意中用到:
$ git grep humanReadableByteCount
问题
你肯定在想:这段代码有什么问题:
再来看一次:
public static String humanReadableByteCount(long bytes, boolean si) {int unit = si ? 1000 : 1024;if (bytes < unit) return bytes + " B";int exp = (int) (Math.log(bytes) / Math.log(unit));String pre = (si ? "kMGTPE" : "KMGTPE").charAt(exp-1) + (si ? "" : "i");return String.format("%.1f %sB", bytes / Math.pow(unit, exp), pre);}
在EB(10^18)之后是ZB(10^21)。是不是因为kMGTPE字符串的越界问题?并不是。long的最大值为2^63-1,大约是9.2x10^18,所以long绝对不会超过EB。
是不是SI和二进制的混合问题?不是。前一个版本的确有这个问题,不过很快就修复了。
是不是因为exp为0会导致charAt(exp-1)出错?也不是。第一个if语句已经处理了该情况。exp值至少为1。
是不是一些奇怪的舍入问题?对了……

许多9
这段代码在1MB之前都非常正确。但当输入为999,999时,它(在SI模式下)会给出“1000.0 kB”。尽管999,999与1,000x1000^1的距离比与999.9x1000^1的距离更小,但根据问题的定义,有效数字部分的1,000是不正确的。正确结果应为"1.0 MB"。
据我所知,原帖下的所有22个答案(包括一个使用Apache Commons和Android库的答案)都有这个问题(或至少是类似的问题)。
那么怎样修复呢?首先,我们注意到指数(exp)应该在字节数接近1x1,000^2(1MB)时,将返回结果从k改成M,而不是在字节数接近999.9x1000^1(999.9k)时。这个点上的字节数为999,950。类似地,在超过999,950,000时应该从M改成G,以此类推。
为了实现这一点,我们应该计算该阈值,并当bytes大于阈值时增加exp的结果。(对于二进制的情况,由于阈值不再是整数,因此需要使用ceil进行向上取整)。
if (bytes >= Math.ceil(Math.pow(unit, exp) * (unit - 0.05)))exp++;

更多的9
但是,当输入为999,949,999,999,999,999时,结果为1000.0 PB,而正确的结果为999.9 PB。从数学上来看这段代码是正确的,那么问题除在何处?
此时我们已经达到了double类型的精度上限。
关于浮点数运算
根据IEEE 754的浮点数表示方法,接近0的数字非常稠密,而很大的数字非常稀疏。实际上,超过一半的值位于-1和1之间,而且像Long.MAX_VALUE如此大的数字对于双精度来说没有任何意义。用代码来表示就是
double a = Double.MAX_VALUE;double b = a - Long.MAX_VALUE;System.err.println(a == b); // prints true
有两个计算是有问题的:
String.format参数中的触发
对exp的结果加一时的阈值
当然,改成BigDecimal就行了,但这有什么意思呢?而且改成BigDecimal代码也会变得更乱,因为标准API没有BigDecimal的对数函数。
缩小中间值
对于第一个问题,我们可以将bytes值缩小到精度更好的范围,并相应地调整exp。由于最终结果总要取整的,所以丢弃最低位有效数字也无所谓。
if (exp > 4) {bytes /= unit;exp--;}
调整最低有效比特
对于第二个问题,我们需要关心最低有效比特(999,949,99...9和999,950,00...0等不同幂次的值),所以需要使用不同的方法解决。
首先注意到,阈值有12种不同的情况(每个模式下有六种),只有其中一种有问题。有问题的结果的十六进制表示的末尾为D00。如果出现这种情况,只需要调整至正确的值即可。
long th = (long) Math.ceil(Math.pow(unit, exp) * (unit - 0.05));if (exp < 6 && bytes >= th - ((th & 0xFFF) == 0xD00 ? 51 : 0))exp++;
由于需要依赖于浮点数结果中的特定比特模式,所以需要使用strictfp来保证它在任何硬件上都能运行正确。

负输入
尽管还不清楚什么情况下会用到负的字节数,但由于Java并没有无符号的long,所以最好处理复数。现在,-10,000会产生-10000 B。
引入absBytes变量:
long absBytes = bytes == Long.MIN_VALUE ? Long.MAX_VALUE : Math.abs(bytes);表达式如此复杂,是因为-Long.MIN_VLAUE == LONG.MIN_VALUE。以后有关exp的计算你都要使用absBytes来代替bytes。

最终版本
下面是最终版本的代码:
// From: https://programming.guide/worlds-most-copied-so-snippet.htmlpublic static strictfp String humanReadableByteCount(long bytes, boolean si) {int unit = si ? 1000 : 1024;long absBytes = bytes == Long.MIN_VALUE ? Long.MAX_VALUE : Math.abs(bytes);if (absBytes < unit) return bytes + " B";int exp = (int) (Math.log(absBytes) / Math.log(unit));long th = (long) Math.ceil(Math.pow(unit, exp) * (unit - 0.05));if (exp < 6 && absBytes >= th - ((th & 0xFFF) == 0xD00 ? 51 : 0)) exp++;String pre = (si ? "kMGTPE" : "KMGTPE").charAt(exp - 1) + (si ? "" : "i");if (exp > 4) {bytes /= unit;exp -= 1;}return String.format("%.1f %sB", bytes / Math.pow(unit, exp), pre);}
这个答案最初只是为了避免循环和过多的分支的。讽刺的是,考虑到各种边界情况后,这段代码比原答案还难懂了。我肯定不会在产品中使用这段代码。

总结
Stack Overflow上的代码就算有几千个赞也可能有问题。
要测试所有边界情况,特别是对于从Stack Overflow上复制粘贴的代码。
浮点数运算很难。
复制代码时一定要注明来源。别人可以据此提醒你重要的事情。
原文链接:https://programming.guide/worlds-most-copied-so-snippet.html
声明:本文由CSDN翻译,转载请注明来源。

☞“去了太空就别回来了!”贝索斯还没“上天”,就遭美国 5 万多人请愿:不准重返地球
☞字节跳动1/3员工不支持取消大小周!库克称iPhone将采用可回收材料生产;清华博士接亲被要求现场写代码|极客头条
关注公众号:拾黑(shiheibook)了解更多
赞助链接:
关注数据与安全,洞悉企业级服务市场:https://www.ijiandao.com/
四季很好,只要有你,文娱排行榜:https://www.yaopaiming.com/
让资讯触达的更精准有趣:https://www.0xu.cn/
 关注网络尖刀微信公众号
关注网络尖刀微信公众号随时掌握互联网精彩









 微信扫码关注公众号
微信扫码关注公众号